Passwords, fun with numbers

When I was on holiday, I saw the number-lock on my suitcase. It has three dials of decimal combination, to support a thousand different combinations. Three dials, ten options each.

Number-lock

That’s when my insane brain started thinking: what if it were the other way around? Instead of a three dial lock with ten options, have a ten-dial lock of three combinations each? What would be better for the number of possible combinations? Length or complexity? More dials or more options?

Reverse number-lock

The total number of combinations for these locks can be calculated by the formula O ^ L (raised to the power of) where O is the number of options for each character and L is the length of the password. Using this formula, we can calculate:

O = 10
L = 3
10 ^ 3 = 1000

For the fictional long number-lock of ten length, the formula gives these numbers:

O = 3
L = 10
3 ^ 10 = 59049

Let’s take a more practical example. Say we use only lowercase characters and a ten character password.

O = 26
L = 10
26 ^ 10 = 141167095653376

Compare this to a 26 length password using only ten different characters.

O = 10
L = 26
10 ^ 26 = 100000000000000000000000000

That’s a hefty 708.380.373.890 times bigger password-space. Yes, length matters when we’re talking about passwords. Or does it? In this blogpost, I will try to find out to what extent password length will help you create safer and stronger passwords.

Disclaimer

In the examples below, I do not use any optimization techniques. The system cracks passwords, simply by trying all theoretical possibilities in a given pattern. In real life, attackers will use lists of leaked passwords, variants of these passwords, combinations of words, different variants of l33tsp34k etc. to optimize and save a lot of time. Some patterns listed will reflect this, for instance ‘Random18’ is an 8 character pattern that starts with an uppercase character, five lowercase characters and two decimals. This often-used patterns still enables a password-space of 30891577600 options. However a fully random 8-character password using uppercase, lowercase and decimals (see ‘8x Alphanumeric’) could theoretically have 218340105584896 different passwords, an increase of a factor 7000 times. When choosing passwords, use fully randomized strings of characters preferably generated by cryptographically random password generators found in password managers for example. Creating strong passwords is all about randomness. Using patterns to derive your password or (please don’t tell me you still do) password-reuse will dramatically decrease the time needed to crack certain passwords.

Other techniques to battle these sort of attacks are also not used. Using proper (dynamic) salting and peppering (static salting) would make the attack described below much harder. Login-throttling will (semi-) prevent an attack on the actual login-system, but that’s an online attack, which is not a practical option for brute-forcing.

While SHA-1, MD5 and reduced forms of SHA2 have design flaws and can be attacked, these flaws cannot be used to reverse a hashed password.

Also using quantum computing to crack passwords is left out of scope.

Basics

Let’s take a password storage system that has at least hashed its passwords. There are several different hashing options, some of which are better suited for passwords than others. We’ll see in a moment why that is. Say this system somehow leaks its user-database. Since passwords are hashed (I hope), this will not immediately reveal the actual passwords of user-accounts. It will however enable attackers to start cracking passwords offline.

Brute-force

Obviously, when attackers use brute-forcing techniques to crack a password, the bigger the password-space is, the longer it will take for cracking a password. That’s where my statistics fetish went in overdrive.

Speed

Depending on password length, complexity and the hash-function, brute-forcing passwords can take anywhere between seconds and many millenia. Let’s see some statistics from a $5000,- cracking rig.

HASHCAT v3.2

OpenCL Platform #1: Intel(R) Corporation
========================================
* Device #1: Intel(R) Xeon(R) CPU E5-2620 v3 @ 2.40GHz, skipped

OpenCL Platform #2: NVIDIA Corporation
======================================
* Device #2: GeForce GTX 1070, 2036/8145 MB allocatable, 15MCU
* Device #3: GeForce GTX 1070, 2036/8145 MB allocatable, 15MCU
* Device #4: GeForce GTX 1070, 2036/8145 MB allocatable, 15MCU
* Device #5: GeForce GTX 1070, 2036/8145 MB allocatable, 15MCU

Hashtype: MD5
Speed.Dev.#*.....: 76526.9 MH/s

Hashtype: SHA1
Speed.Dev.#*.....: 25963.3 MH/s

Hashtype: SHA256
Speed.Dev.#*.....: 9392.1 MH/s

Hashtype: SHA512
Speed.Dev.#*.....: 3235.0 MH/s

Hashtype: scrypt
Speed.Dev.#*.....: 1872.4 kH/s

Hashtype: bcrypt, Blowfish(OpenBSD)
Speed.Dev.#*.....: 43551 H/s

Source: Netmux.com

This machine will crack (brute-force, no optimization) the full password space of most of these fictional password-patterns in seconds.

Hash-type	3x Number-lock	Reverse Number-lock	10x Lowercase	Pattern like ‘Random18’	8x Alphanumeric
MD5	0 seconds	0 seconds	30 minutes	0 seconds	47 minutes
SHA1	0 seconds	0 seconds	1 hours	0 seconds	2 hours
SHA256	0 seconds	0 seconds	4 hours	0 seconds	6 hours
SHA512	0 seconds	0 seconds	12 hours	0 seconds	18 hours
SCRYPT	0 seconds	0 seconds	2 years	1 seconds	3 years
BCRYPT	0 seconds	1 seconds	102 years	1 minutes	158 years

If we include some more complex and/or larger password-patterns, the numbers quickly become unimaginably large. So large, that even Java double was by far not suitable to calculate these numbers. But BigInteger saved me:

	4x English words	4x Dictionary Words	8x All alphanumeric	10x All alphanumeric	14x All alphanumeric	26x numerical	10x ASCII	8x UTF8 (smilies ;-)	42x numerical	30x alphanumeric or symbol	30x UTF8
MD5	226 days	358 years	47 minutes	126 days	5138 millennia	41436 millennia	489 years	51421389666782902409 millennia	414361381210588518603 millennia	88938014688729074768127408015877045392 millennia	5235959597778261501539031063423676185261821165413036824455971255837835566976203833828094413552079731849234334321635613864542157766366 millennia
SHA1	1 years	1 millennia	2 hours	1 years	15146 millennia	122133 millennia	1 millennia	151564691117497717717 millennia	1221331340151852287818 millennia	262145049214965009527795362703902087372 millennia	15433005686612150231369944355591058342426150071194606531583414538921341225900838998547149182748674106575557459151894268396175804045363 millennia
SHA256	5 years	2 millennia	6 hours	2 years	41871 millennia	337621 millennia	3 millennia	418981861872310611515 millennia	3376219587074731583385 millennia	724667598969655458510131849159423458553 millennia	42662637380694119536858346513294931385090966039910874858813222463386937814805129116063414824848399232466985123582412501852666736211388 millennia
SHA512	14 years	8 millennia	18 hours	8 years	121563 millennia	980209 millennia	11 millennia	1216420261171848066281 millennia	9802099531302808811224 millennia	2103910527444482544628441836318460916561 millennia	123861439426033149954289729918861615165969972841869220328117362194243109320071484751461885124098500906106080673631646509629190495570627 millennia
SCRYPT	25 millennia	14642 millennia	3 years	14 millennia	210028588 millennia	1693537277 millennia	19993 millennia	2101644704598872299946099 millennia	16935372774922338444943672 millennia	3634987479322207344516668094686082602583640 millennia	213999015457817368138286304362057960404781490142836427986252759398833827521059203787107027545641236077362300245245875058027361275993900447 millennia
BCRYPT	1092 millennia	629518 millennia	158 years	611 millennia	9029816284 millennia	72810709246 millennia	859597 millennia	90356582969183910689055971 millennia	728107092460898406565004976 millennia	156280006343893390091456208594296825907042533 millennia	9200517933990430532068776291876588943122152468219947366569301891997346987449915114945218212588887750711881954012499746473110405115174834065 millennia

Although these numbers look very impressive, they are far from meaningful.

Length

Then I saw a Tweet by Jeremi M Gosney, founder and CEO of Terahash. Terahash builds professional hashcrack-servers with 40-ish GPU’s costing 10-100k. Clients are state-actors like secret service and intelligence agencies.

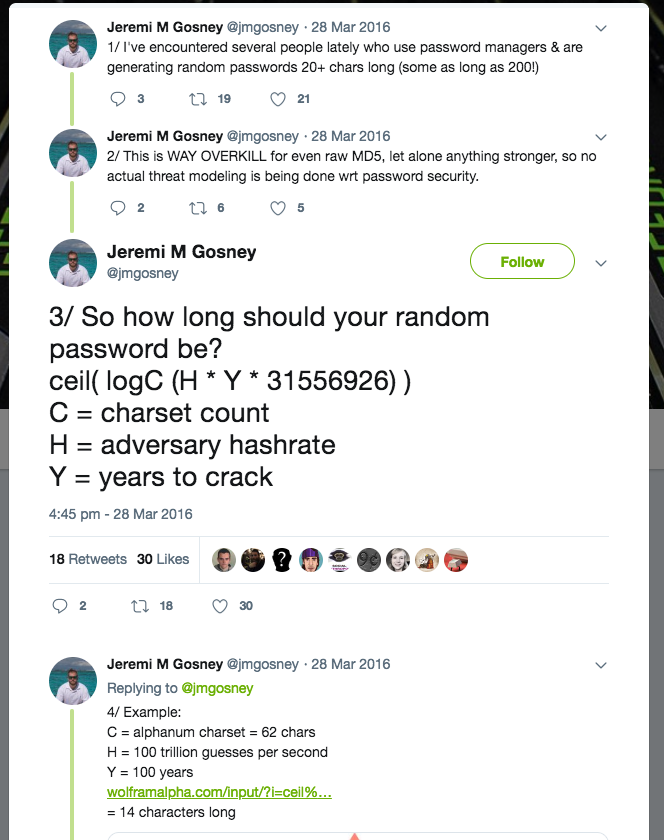
With a bit of tinkering (there’s no logC method in Java / Groovy), I’ve come up with this:

    int requiredLength(MaskSymbol pattern, BigInteger years, BigInteger speed) {
        return Math.ceil( logX(pattern.options, (speed * years * ExtraLongDuration.SECONDS_IN_YEAR)))
    }

    static double logX(long x, double a) {
        return Math.round(Math.log(a) / Math.log(x));
    }

This will calculate for each password-pattern and hash-function, the required length for a given minimum time to crack. I’ve chosen 100 years for this, here are the results:

	Decimal	Lowercase	UPPERCASE	Alphanumeric	ASCII	Symbol	Alphanumeric or symbol	UTF8	English words	Dictionary Words	USA Cities	Cities
MD5	20	14	14	11	10	13	10	4	4	4	5	3
SHA1	20	14	14	11	9	13	10	4	4	4	4	3
SHA256	19	14	14	11	9	13	10	4	4	4	4	3
SHA512	19	13	13	11	9	13	10	4	4	4	4	3
SCRYPT	16	11	11	9	7	10	8	3	3	3	4	3
BCRYPT	14	10	10	8	7	9	7	3	3	3	3	2

As you can see, password-length quickly adds so much password-space that cracking a sufficiently randomized password is almost impossible to crack with a $5000,- cracking-rig.

Professional cracking

But what about a more professional cracking-rig. Let’s see what a $21200,- machine would do. Here are its benchmarks and below are both the speeds and minimum required password-length for at least 100 years to crack.

	3x Number-lock	Reverse Number-lock	10x Lowercase	Pattern like ‘Random18’	4x English words	4x Dictionary Words	8x All alphanumeric	10x All alphanumeric	14x All alphanumeric	26x numerical	10x ASCII	8x UTF8 (smilies ;-)	42x numerical	30x alphanumeric or symbol	30x UTF8
MD5	0 seconds	0 seconds	4 minutes	0 seconds	31 days	49 years	6 minutes	17 days	715 millennia	5768 millennia	68 years	7158667536639855365 millennia	57685632133462955256 millennia	12381572778393489233896687903384065972 millennia	728928063567795597784477490062793023579976099951695338842022315259917152356614977571364741452535292761966838237581183297526707755450 millennia
SHA1	0 seconds	0 seconds	23 minutes	0 seconds	171 days	270 years	35 minutes	95 days	3882 millennia	31302 millennia	369 years	38846194915014101623 millennia	313028548704487527189 millennia	67188060772782833483445304447090040129 millennia	3955496115925145509399084662265718904856000613459495831801181309954357933370496082635530092561289737722143839873626618545413931423208 millennia
SHA256	0 seconds	0 seconds	59 minutes	0 seconds	1 years	698 years	1 hours	247 days	10014 millennia	80749 millennia	953 years	100208293095665543512 millennia	807493671504137738399 millennia	173319443543392591480211292774787011389 millennia	10203663833499295637369740212163092001963688320764944912870063375003856912772572363493692248327161872380356485691107489766852339306711 millennia
SHA512	0 seconds	0 seconds	3 hours	0 seconds	3 years	2 millennia	4 hours	2 years	30150 millennia	243111 millennia	2 millennia	301696621628800111506 millennia	2431117277358075525696 millennia	521812007412457049356605256376087421517 millennia	30720121176636069100774135095222629630684938791827752774333157000021195452870918645663229272995227467838136896276124635533218683398448 millennia
SCRYPT	0 seconds	0 seconds	257 days	0 seconds	7 millennia	4315 millennia	1 years	4 millennia	61896203 millennia	499091712 millennia	5892 millennia	619362484440218540083273 millennia	4990917129733939797641068 millennia	1071244283667726612398364577081958143555144 millennia	63066303068106908019536834231135173536147456070425266036272867978024153403703667769100369619337160688007109621342311554049017274442587423 millennia
BCRYPT	0 seconds	0 seconds	24 years	18 seconds	257 millennia	148355 millennia	37 years	144 millennia	2128016931 millennia	17158978346 millennia	202577 millennia	21293936931227968043393271 millennia	171589783461929580651041838 millennia	36829819027504875713598535392263101001502215 millennia	2168245435839920130422766646577474702715978691252418440267638889060478672350818469539930727145339017485136206597393812005684151802873264060 millennia

As you can see, the time required to crack these password-patterns decreases dramatically. A 10-length lowercase password becomes within reach even when hashed with scrypt. An 8-length alphanumeric (no symbols!) password can be cracked within hours if no proper ‘slow’ hash-function is used. What’s more suprising though, is the difference in length to ‘fix’ these speed-gains.

	Decimal	Lowercase	UPPERCASE	Alphanumeric	ASCII	Symbol	Alphanumeric or symbol	UTF8	English words	Dictionary Words	USA Cities	Cities
MD5	21	15	15	12	10	14	11	4	5	4	5	3
SHA1	21	14	14	11	10	14	10	4	5	4	5	3
SHA256	20	14	14	11	10	13	10	4	4	4	5	3
SHA512	20	14	14	11	9	13	10	4	4	4	4	3
SCRYPT	16	12	12	9	8	11	8	3	4	3	4	3
BCRYPT	15	10	10	8	7	10	7	3	3	3	3	2

Yes, you only need a single extra character in length for each of these combinations to make your password strong enough again. Let’s add some more $$ to our machine, to illustrate Moore’s law of decreasing hardware-prices (yes I know, that’s not Moore’s law, but it extends from Moore’s law). Let’s take a hypothetical 40 Brutalis machines (currently about $847000,-). Since cracking passwords is perfectly suited for parallel execution, we can just multiply the speeds of this machine with 40 and rerun our calculations.

	3x Number-lock	Reverse Number-lock	10x Lowercase	Pattern like ‘Random18’	4x English words	4x Dictionary Words	8x All alphanumeric	10x All alphanumeric	14x All alphanumeric	26x numerical	10x ASCII	8x UTF8 (smilies ;-)	42x numerical	30x alphanumeric or symbol	30x UTF8
MD5	0 seconds	0 seconds	6 seconds	0 seconds	18 hours	1 years	9 seconds	10 hours	17 millennia	144 millennia	1 years	178966688415996384 millennia	1442140803336573881 millennia	309539319459837230847417197584601649 millennia	18223201589194889944611937251569825589499402498792383471050557881497928808915374439284118536313382319049170955939529582438167693886 millennia
SHA1	0 seconds	0 seconds	34 seconds	0 seconds	4 days	6 years	53 seconds	2 days	97 millennia	782 millennia	9 years	971154872875352540 millennia	7825713717612188179 millennia	1679701519319570837086132611177251003 millennia	98887402898128637734977116556642972621400015336487395795029532748858948334262402065888252314032243443053595996840665463635348285580 millennia
SHA256	0 seconds	0 seconds	1 minutes	0 seconds	11 days	17 years	2 minutes	6 days	250 millennia	2018 millennia	23 years	2505207327391638587 millennia	20187341787603443459 millennia	4332986088584814787005282319369675284 millennia	255091595837482390934243505304077300049092208019123622821751584375096422819314309087342306208179046809508912142277687244171308482667 millennia
SHA512	0 seconds	0 seconds	4 minutes	0 seconds	33 days	52 years	6 minutes	18 days	753 millennia	6077 millennia	71 years	7542415540720002787 millennia	60777931933951888142 millennia	13045300185311426233915131409402185537 millennia	768003029415901727519353377380565740767123469795693819358328925000529886321772966141580731824880686695953422406903115888330467084961 millennia
SCRYPT	0 seconds	0 seconds	6 days	0 seconds	187 years	107 millennia	9 days	104 years	1547405 millennia	12477292 millennia	147 millennia	15484062111005463502081 millennia	124772928243348494941026 millennia	26781107091693165309959114427048953588878 millennia	1576657576702672700488420855778379338403686401760631650906821699450603835092591694227509240483429017200177740533557788851225431861064685 millennia
BCRYPT	0 seconds	0 seconds	221 days	0 seconds	6 millennia	3708 millennia	341 days	3 millennia	53200423 millennia	428974458 millennia	5064 millennia	532348423280699201084831 millennia	4289744586548239516276045 millennia	920745475687621892839963384806577525037555 millennia	54206135895998003260569166164436867567899467281310461006690972226511966808770461738498268178633475437128405164934845300142103795071831601 millennia

Again, we can see some password-patterns fall to the sheer speed of this machine, including a 10-length lowercase password at even scrypt or bcrypt, a pass-phrase of four English words and even 10-length alphanumeric passwords fall within days if not properly hashed. But how many longer should our passwords be with this 40x increase in computing power?

	Decimal	Lowercase	UPPERCASE	Alphanumeric	ASCII	Symbol	Alphanumeric or symbol	UTF8	English words	Dictionary Words	USA Cities	Cities
MD5	23	16	16	13	11	15	12	4	5	4	5	4
SHA1	22	16	16	12	10	15	11	4	5	4	5	4
SHA256	22	15	15	12	10	14	11	4	5	4	5	3
SHA512	21	15	15	12	10	14	11	4	5	4	5	3
SCRYPT	18	13	13	10	8	12	9	3	4	3	4	3
BCRYPT	16	12	12	9	8	11	8	3	4	3	4	3

Yes, two extra characters at most.

Conclusion

Fully random passwords are really hard to crack. Even with costly, high-grade and specialized hardware, a moderately strong password cannot be cracked in a reasonable timeframe. Using all characters available, including both uppercase, lowercase, decimals and symbols, even a 15 character password is sufficiently strong against brute-force attacks. Even while hardware becomes increasingly cheaper and faster, increasing password length with just a few extra characters is sufficient to resist faster hardware.

Knowing this, we can conclude that the most important factor in password-safety is randomness. Reuse of passwords, patterns like ‘Random18’ or ‘Password-ebay’ is absolutely devastating to the protection passwords offer. Using longer passwords is always a good idea, but anywhere above 15 to 20 positions is overkill and it will be for many many years (unless quantum computing becomes a thing?).

To manage fully random passwords of 15 to 20 length, the use of password managers is highly advisable. These can also be used to help generate sufficiently randomized passwords.

Terminology explained

Term	Explanation
3x Number-lock	Lock using dials with decimals. Each of 3 position normally has 10 options, 0 to 9.
Reverse Number-lock	Fictional lock with 10 positions of 3 options each. To illustrate the difference with a 3x number-lock.
‘Random18’	A password pattern starting with an uppercase, then five lowercase letters and two decimals. Fits most password policies
English words	An average adult knows about 35k words. source
English Dictionary	There are about 171k words in the English language. source
Alphanumeric	All letters, uppercase and lowercase and all decimals for a total of 62 options.
Numerical / Decimal	All decimals, 10 options.
ASCII	All ASCII characters, which are 128.
UTF8	There currently are about 137k printable, non-control characters in UTF8. These include smilies and other graphical symbols.
Lowercase	All characters in lowercase. 26 options.
UPPERCASE	All characters in uppercase. 26 options.
Symbol	The set of symbols normally allowed in passwords: *!”#$%&’()+,-./:;<=>?@[]^_{}~\ \|`** (including space)
Alphanumeric or symbol	For a total of 95 options.
USA Cities	There are about 27k USA cities. source
Cities	The estimate for cities in the world is 2M. source

Acknowledgements

Thank you for inspiration, input and comments to:

Arjan Gelderblom for helping me get started on Sec App Development
Jeremy M Gosney for inspiring me on hashcracking and benchmarking awesome hardware
Jim Manico for helping me understand Sec App Development and just being an awesome dude
John Opdenakker for discussing password- and identity management
Ronald van der Meer for discussing crypto, password- and identity management and tweeting many relevant news-items

Notes

Calculations made with ComplexityCalculator in my Security-examples Groovy scripts